Differentiate the following functions with respect to x 1 y = 5xln(6x) 2 y = e 5x(4x 2) 3 y = 3x5cos(4x) 4 y = e 4xln(7x) (Solutions on page 9) The Quotient Rule Consider y = v u, where u and v are functions of x, then v2 dx dv u dx du v dx dy − = Example 1 Differentiate y = x 1 x 1 2 2 − u = x 2 – 1 v = x 2 1 dx du = 2x dx dvAn online derivative calculator that differentiates a given function with respect to a given variable by using analytical differentiation A useful mathematical differentiation calculator to simplify the functions Just copy and paste the below code to your webpage where youThen, y = e^2sinx Put u = 2sin x Therefore, y = e^u where u = 2 sin x and dy/du = e^u and du/dx = 2 cos x Since dy/dx = dy/du du/dx , dy/dx = e^u (2cos x) Substituting for u dy/dx = e^2sin x 2cos x = 2cos xe^2sin x (Proved)

29 30 If Y E X Sin X Cos X Prove That Frac D 2 Y X 2 2 Frac D Y D 2 Y 0
Differentiate y=e^x sin x
Differentiate y=e^x sin x-Differentiate E X Log Sin 2 X ?I think this plan just turned from being a master plan to a MEGAmaster plan



Answered Sin X In X Differentiate The Function Bartleby
Experts are waiting 24/7 to provide stepbystep solutions in as fast as 30 minutes!*Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high 96% (69 ratings) Previous question Next question Get more help from CheggPlease Subscribe here, thank you!!!
Differentiation of y=e^(sinx) wrt to x My method ln both sides and then differientiate is that okay? The chain rule states that d dx f (g(x)) = f '(g(x))g'(x) or, if we pose u = g(x) df dx = df du du dx So in our case if u = sinx dy du = d du eu = eu = esinx du dx = d dx sinx = cosx We can see that in each case, the slope of the curve `y=e^x` is the same as the function value at that point Other Formulas for Derivatives of Exponential Functions If u is a function of x, we can obtain the derivative of an expression in the form e u `(d(e^u))/(dx)=e^u(du)/(dx)` If we have an exponential function with some base b, we have the following derivative
CBSE CBSE (Arts) Class 12 Question Bank Solutions Concept Notes & Videos 533 Time Tables 18 Syllabus Advertisement Remove all ads Differentiate E X Log Sin 2 X ?Given that y = log(sinx), we need to find the value of dxdy We know that the derivative of log(x) wrt x is x1 dxdy = dxd (log(sinx)) = sinx1 × dxd (sinx) = sinx1 ×cosx= cotxHence, dxdy = cotx\Let y = e^{\sin}\sqrt{x} \ \\text{Differentiate it with respect to x we get}, \ \\frac{d y}{d x} = \frac{d}{dx}\left( e^{\sin}\sqrt{x} \right)\




For Given Below Verify That The Given Function Implicit Or Explicit Is A Solution Of The Corresponding Differential Equation Y E X Acos X B Sin X D 2y Dx 2 2




Differentiate E Sinx Wit Respect To Cos X
Ex 54, 1 Differentiate 𝑤𝑟𝑡 𝑥 in , 𝑒^𝑥/sin𝑥 Let 𝑦 = 𝑒^𝑥/sin𝑥 Let 𝑢 =𝑒^𝑥 & 𝑣 = sin𝑥 ∴ 𝑦 = 𝑢/𝑣 Differentiating both sides 𝑤𝑟𝑡𝑥 𝑑(𝑦)/𝑑𝑥 = 𝑑(𝑢/𝑣)/𝑑𝑥 𝑑𝑦/𝑑𝑥 = ((𝑢)^′ 𝑣 − 〖𝑣 〗^′ 𝑢)/𝑣^2 𝑑𝑦/𝑑𝑥 = ((𝑢)^′ 𝑣 − 〖𝑣 〗^′ 𝑢)/𝑣Differentiation y=a^x To find the derivative of y=a^x, we use the exact same steps as that used for differentiating y=e^x, and y=x^x as well Hence, if you did those earlier you should be able to do this one Just as before, you take the log on both sides This brings the x down from the power position, as shown on the RHSThen y = e^u so dy/du = e^u;




Differentiate E Sinx Wit Respect To Cos X Youtube



Find Dy Dx If Y E Sin 2 X 2tan 1 1 X 1 X Sarthaks Econnect Largest Online Education Community
Free implicit derivative calculator implicit differentiation solver stepbystep This website uses cookies to ensure you get the best experience By using thisThis calculus video explains how to find the derivative of x^x^x using a technique called logarithmic differentiation which is useful for differentiating expSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




Ipe Material Notes
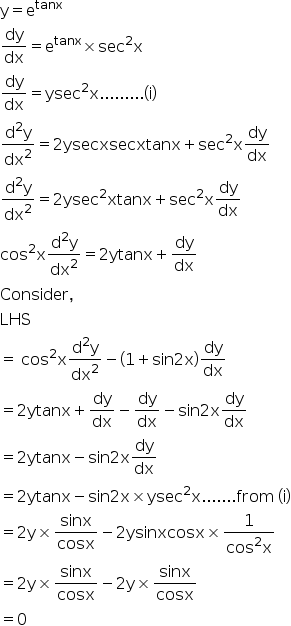



If Y Etan X Prove That Cos2 X D2y Dx2 1 Sin 2x Dy Dx 0 Explain In Great Detail Mathematics Topperlearning Com Mbti5k33
Find the derivative {eq}y = e^{2x} \sin 3x {/eq} Derivative Product Rule The derivative of a function measures the amount at which a function changes when its variable also changes Ex 54, 2 (Method 1) Differentiate 𝑤𝑟𝑡 x in , 𝑒^(sin^(−1) 𝑥)Let 𝑦 = 𝑒^(sin^(−1) 𝑥) Differentiating both sides 𝑤𝑟𝑡𝑥 𝑑(𝑦)/𝑑𝑥 = 𝑑(𝑒^(sin^(−1) 𝑥) )/𝑑𝑥 𝑑𝑦/𝑑𝑥 = 𝑒^(sin^(−1) 𝑥) Differentiate y=e^x cos〖x^2 〗 Pinoybixorg is an engineering education website maintained and designed toward helping engineering students achieved their ultimate goal to become a fullpledged engineers very soon




If Y E Sinx Then The Value Of Dy Dx Is




Ex 5 4 1 Differentiate Ex Sinx Chapter 5 Ncert Ex 5 4
The expression for the derivative is the same as the one for the original function That is The derivative of e x is e x The derivative of e x is e x This is one of the properties that makes the exponential function really important Now you can forget for a while the series expression for the exponential We only needed it here to prove the2 Write cos (x 3) as cos (x^3) 6 Ensure that the input string is as per the rules specified above An online logarithmic differentiation calculator to differentiate a function by taking a log derivative Code to add this calci to your website Just copy and paste the below code to your webpage where you want to display this calculatorTl;dr I'll just answer the question in the title Ans 2 cos 2x by using the chain rule with f (x) = 2x (therefore f' (x)=2) If y=sin f (x) then =f' (x)cosf (x) Wow, youve been (deceived)^2 Even after seeing everything ive written, youre still answering the question!




Differentiate E Sinx With Respect To X By First Principal Maths Continuity And Differentiability Meritnation Com




Find The Derivative Of Y E X Sinx 1 Logx Youtube
X = k π 2 x = k 2 π 2 4, k ∈ I So you can see the first critical point is when k=1, and then we have From the cos equation x = k 2 π 2 4 x = π 2 4 ≈ 247 Which you can see is the first peak in the graph, From the sin equation x = k 2 π 2 x = π 2 ≈ 987 Which is the second peak in the graph, at about xAlgebra Find dy/dx y=e^ (3x)sin (2x) y = e3x sin(2x) y = e 3 x sin ( 2 x) Differentiate both sides of the equation d dx (y) = d dx (e3x sin(2x)) d d x ( y) = d d x ( e 3 x sin ( 2 x)) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more stepsDifferentiate y = xsin (x) This is a function which is in the form, y = f (x)g (x) It's the product of two functions and so we must make use of the product rule This is a simple formula which you have to remember dy/dx = f' (x)g (x) f (x)g' (x) In words the derivative of first function multiplied by the original second function, plus, the derivative of the second function multiplied by the original




Derivative Of X Into E Power X Into Sin X Brainly In



How To Find The Differentiate E X Sin 3x Chain Rule Derivative Collection Ap Calc Calculus Cr 16 Youtube
This is just the chain rule You have a composite function A function is a machine that takes an input and produces an output The first machine is the log function (I assume the base is mathe/math—IDifferentiate y=e^{\sin e^{x}} Join our free STEM summer bootcamps taught by experts Space is limited 1 There are two ways of doing this First, e is a constant This means that the exponent rule applies here Combining that with the chain rule yields y = (1 − sin(x))e → y ′ = e ⋅ (1 − sin(x))e − 1 ⋅ ( − cos(x)) Second, we may take the logarithm of both sides to find another convenient form and then use the various derivative




Integral Calculation Indefinite Integral Differentiation Rules If F X X 6 4x 2 18x 90 F X 6x 5 8x 18 Multiply By The Power Than Subtract Ppt Download



Implicit And Logarithmic Differentiation
The Derivative of y = sin x Graph the function y = sin x and its derivative Examine the graph of the derivative and determine how it relates to the graph of the function The Derivative of y = e x Another derivative that is easily found by graphing is that of y = e x Enter Y 1 = e^(X) and Y 2 = nDeriv(Y 1,X,X) e^( is the "2 nd" featureSolution for Differentiate y= e^sin^1 x Want to see this answer and more? Let u = e x sin^2 x and v = (sin x) x So that y = u v Now, u = e x sin^2 x, Differentiating both sides wrt x, we get ⇒ \(\frac{du}{dx}\) = e x sin^2 x x(sin 2x) sin 2 x ( 2) Also, v = (sin x) x ⇒ log v = x log (sin x) Differentiating both sides wrt x, we get Substituting from − (2), − (3) in − (1) we get



If Y E X A Cos X B Sin X Then Y Is A Solution Of Studyrankersonline



If Y E Xsinx 3 Tanx X Then Find Dy Dx Sarthaks Econnect Largest Online Education Community
In this math video lesson I review how to find the derivative of y=x^2*sinx This is a common derivative that requires the product rule #derivatives #prodD x d y = e s i n y cos y 1 2 x Explanation Differentiate both sides Recall that the chain rule will be put Recall that the chain rule will be put Lipschitz constant for f(x,y)=e^x \sin yIe ln y = sinx ln e = sinx 1/y (dy/dx) = cosx dy/dx = (cosx)(e^sinx) OR I put u = sin x so du/dx = cos x;
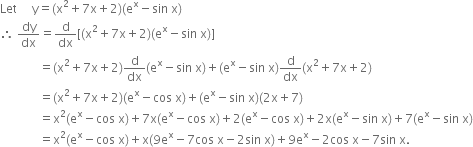



Differentiate X2 7 X 2 Ex Sin X W R T X Zigya



Users Math Msu Edu Users Magyarp Math133 6 3 Natural Exp Fcn Pdf
E^x times 1 f' (x)= e^ x this proves that the derivative (general slope formula) of f (x)= e^x is e^x, which is the function itself In other words, for every point on the graph of f (x)=e^x, the slope of the tangent is equal to the yvalue of tangent point So if y= 2, slope will be 2 if y= , slope will beIt is a very effective rule to find the derivative easily Let {eq}g\left {a\left( x \right)} \right {/eq} is the complex or composite function, then we can use the following given formula toY = e x sin x On differentiating, we get d x d y = sin x d x d e x e x d x d sin x d x d y = sin x e x e x cos x ∴ d x d y = e x (sin x cos x)



If Y E X Sin X Then Prove That D 2y Dx 2 2dy Dx 2y 0 Sarthaks Econnect Largest Online Education Community




Differentiate Of Esin X Tan X X Maths Continuity And Differentiability Meritnation Com
The derivative of y, given y= sin(x y), with respect to x, using implicit differentiation y'= cos(xy)(1 y') so y' y'cos(xy)= cos(x y) and y'= cos(xy)/(1 cos(xy)) The derivative of x, given y= sin(x y), with respect to y (which is what you told you Diane you want, but I doubt since I would read what you originally wrote as 'the derivative OF y= ), by implicit differentiationThe Derivative Calculator supports computing first, second, , fifth derivatives as well as differentiating functions with many variables (partial derivatives), implicit differentiation and calculating roots/zeros You can also check your answers!Y = d d x ( sin x × log e x) In this differentiation problem, the variable y represents a function in x Hence, it can be differentiated with respect to x and do not think that y is a constant Therefore, the function y can be differentiated by the derivative rule of logarithms 1 y × d y d x = d d x ( sin




Solved A 1 Differentiate Y E Cos X E Sin X B 2xe Chegg Com




Differentiate E Sinx With Respect To X From First Principles
Created by Sal Khan Exponential functions differentiation Derivatives of sin (x), cos (x), tan (x), eˣ & ln (x) This is the currently selected item Derivative of aˣ (for any positive base a) Practice Derivatives of aˣ and logₐx Worked example Derivative of 7^ (x²x) using the chain rule Practice Differentiate exponential functions The derivative of sin x is cos x, The derivative of cos x is −sin x (note the negative sign!) and The derivative of tan x is sec 2x Now, if u = f(x) is a function of x, then by using the chain rule, we have d ( sin u) d x = cos u d u d x//googl/JQ8NysStewart Calculus 34 #40 Differentiate y = e^(sin(2x)) sin(e^(2x))




Ex 5 4 2 Differentiate E Sin 1 X Teachoo Ex 5 4




Ipe Material Notes
What is the derivative of Y=e^sin (logx)?In differential calculus, there is no direct formula to find the derivative of square root of $\sin{x}$ function The $\sqrt{\sin{x}}$ function is a composition of two functions $\sqrt{x}$ and $\sin{x}$ Hence, the differentiation of $\sqrt{\sin{x}}$ can be calculated by the chain ruleCalculus Find dy/dx y=e^ (2x)sin (x) y = e2x sin(x) y = e 2 x sin ( x) Differentiate both sides of the equation d dx (y) = d dx (e2x sin(x)) d d x ( y) = d d x ( e 2 x sin ( x)) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps




29 30 If Y E X Sin X Cos X Prove That Frac D 2 Y X 2 2 Frac D Y D 2 Y 0




Differentiate Wrt X Don T Go Shortcut Esinx Sin Ex Mathematics Topperlearning Com Nodo42rr
Derivative of a Constant lf c is any real number and if f(x) = c for all x, then f ' (x) = 0 for all x That is, the derivative of a constant function is the zero function It is easy to see this geometrically Referring to Figure 1, we see that the graph of the constant function f(xDifferentiate f(x) = x2 sin(x) Expert Answer Who are the experts? y'=e^sin(x)*cos(x) Taking the logarithm on both sides we get ln(y)=sin(x) Differentiating this with respect to x 1/y*y'=cos(x) so y'=e^(sin(x))*cos(x)




If E X Sin Y E Y Cos X 1 Then Frac D Y D X



1
Then dy/dx = (e^u) cos x = cos x e^sin x Now sin x isn't a constant so is this wrong?Video Transcript {'transcript' "So this problem asked us to find the derivative of E to the negative X Times sign of X And because this is the product of two different types of functions being multiplied together, we have to use the product rule and the product will can be summarized as the derivative of the first term times a second term plus that first term times the derivative of theThe derivative is an important tool in calculus that represents an infinitesimal change in a function with respect to one of its variables Given a function , there are many ways to denote the derivative of with respect to The most common ways are and When a derivative is taken times, the notation or is used These are called higherorder




Differentiate X 1 X 3 Novocom Top




Differentiate E Sinx Using First Principle Full Explanation Youtube
Free derivative calculator differentiate functions with all the steps Type in any function derivative to get the solution, steps and graph This website uses cookies to ensure you get the best experience Step 1, Begin with a general exponential function Begin with a basic exponential function using a variable as the base By calculating the derivative of the general function in this way, you can use the solution as model for a full family of similar functions1 X Research source y=ax{\displaystyle y=a^{x}}Step 2, Take the natural logarithm of both sides You need to manipulate the function to help find a standard derivative in terms of the variable x{\displaystyle xMathematics Advertisement Remove Solution Show Solution \\text{Let } y = e^x \log \sin2x\ Differentiate it with respect to x we




Differentiation Of Y E Sinx Brainly In




Rd Sharma Class 12 Maths Solutions Chapter 11 Differentiation
Interactive graphs/plots help visualize and better understand the functions



1




How Do You Find The Derivative Of E Sinx Socratic



Q Tbn And9gcrlw5wx6qxsllz2r9p3fgzffnje5hqap6knkskthxk8e15jx7e4 Usqp Cau




Example 48 Examples




Ex 5 4 2 Differentiate E Sin 1 X Teachoo Ex 5 4
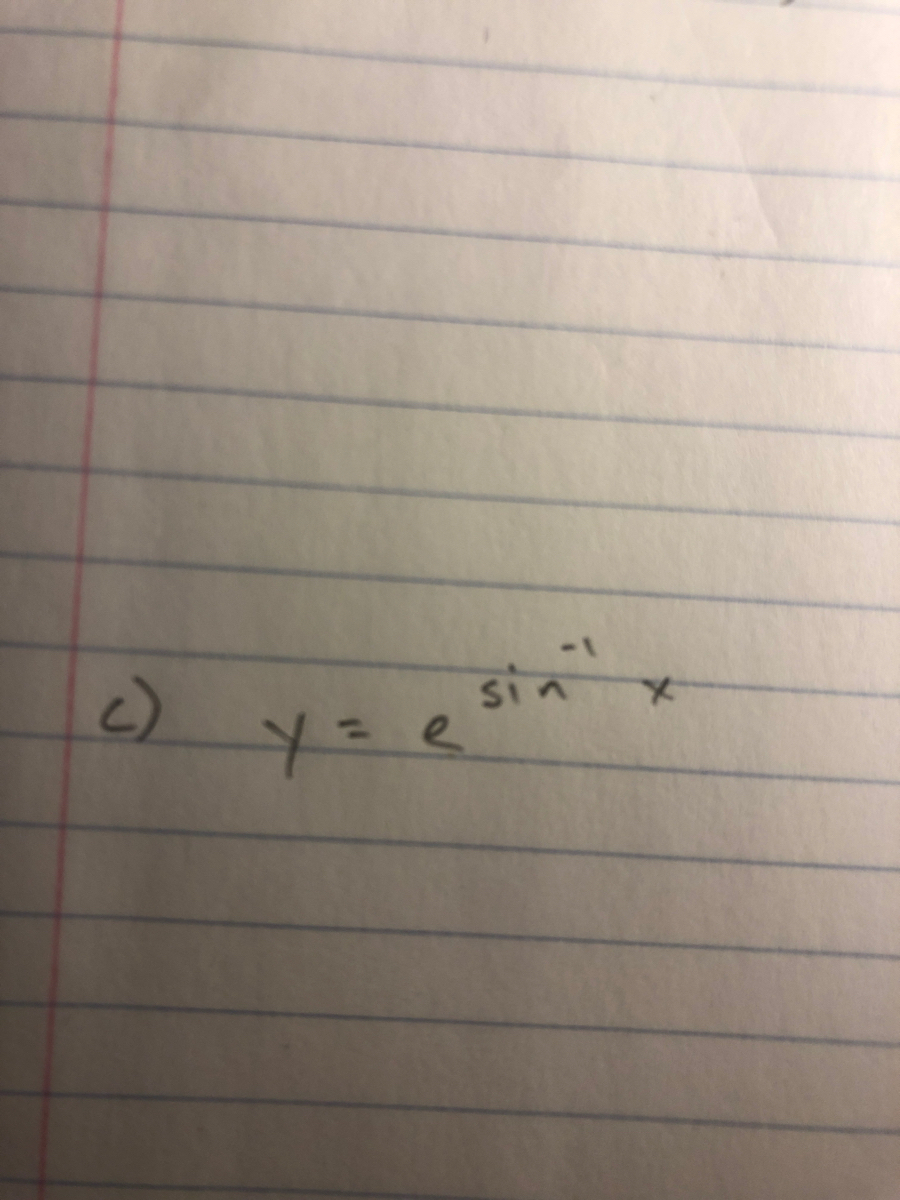



Answered Differentiate Y E Sin 1 X Bartleby




Drill Find Dy Dx Y X 3 Sin 2x Y E 2x Ln 3x 1 Y Tan 1 2x Product Rule X 3 2cos 2x 3x 2 Sin



What Is The Derivative Of E Sinx Socratic




Derivative Chain Rule Examples List 1 Find Dy Dx If A Y U 12
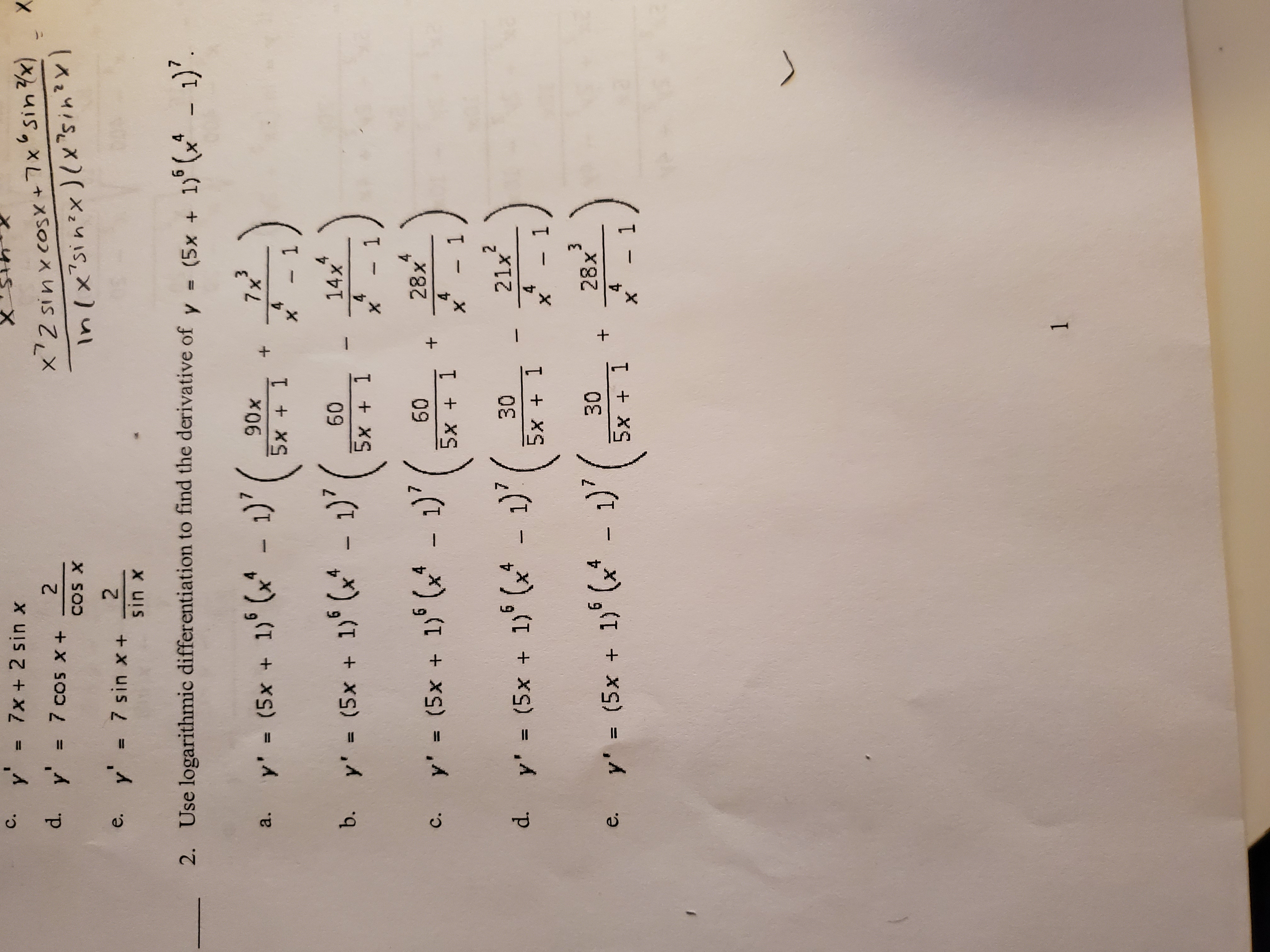



Answered Y 7x 2 Sin X S Yx X72 Sinxcosx 7 Bartleby




If Y E X Sin 2 X Sin X X Find Dy Dx With Video Teachoo




Find The Derivative Of E X Sin X With Respect To X




Ex 5 4 1 Differentiate Ex Sinx Chapter 5 Ncert Ex 5 4




Find The Derivative Using First Principles E Sinx Socratic
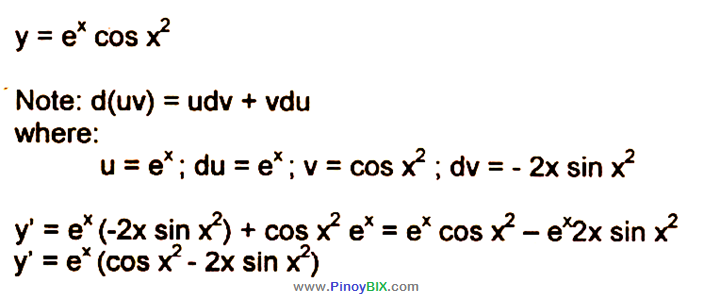



Solution Differentiate Y E X Cos X 2



Derivatives Of Sin X Cos X Tan X Eˣ Ln X Video Khan Academy



If Y E X Cos X Show That D 2y Dx 2 2e X Sin X Sarthaks Econnect Largest Online Education Community




If Y E Sin 2x Then Dy Dx
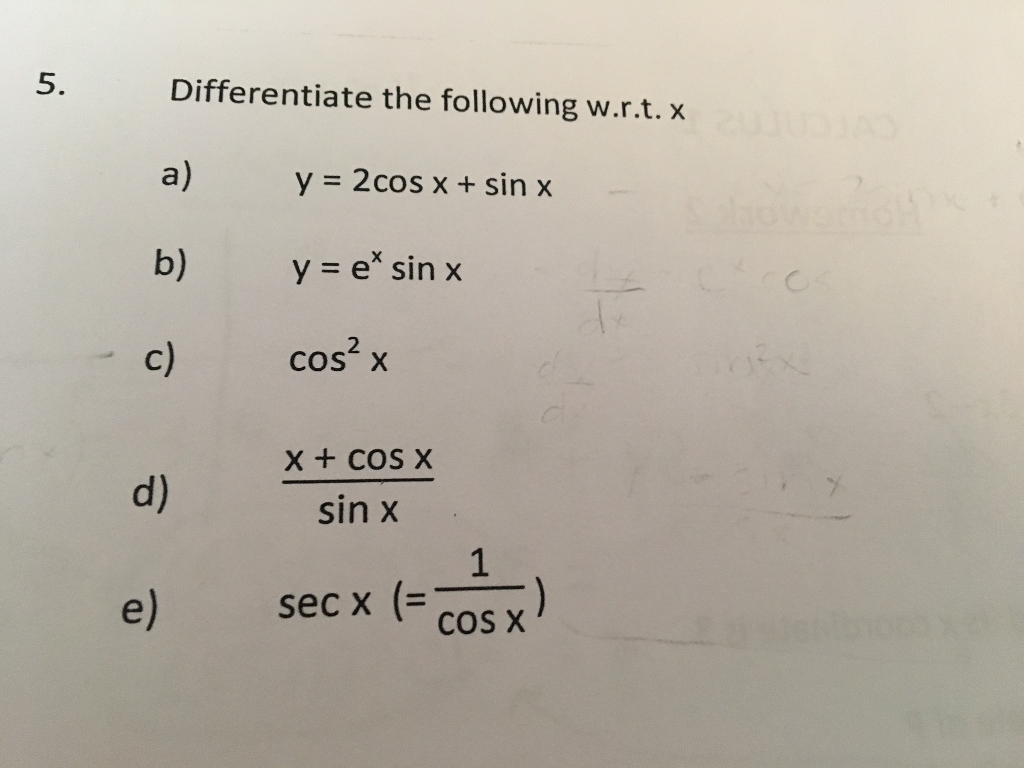



Differentiate The Following W R T X A Y 2cos X Chegg Com



If X Ecos2t And Y Esin2t Prove That Dy Dy Y Log X Log Y Studyrankersonline




Ipe Material Notes




Find The Second Order Derivative Of x Sin 4x Explain In Great Detail Mathematics Topperlearning Com J10h42dd




Example 29 Differentiate I E X Ii Sin Log X Iii Cos 1 E X




Rd Sharma Class 12 Maths Solutions Chapter 11 Differentiation




If Y E X Sin 2 X Sin X X Find Dy Dx With Video Teachoo




Derivative Of 𝑒ˣ Video Khan Academy
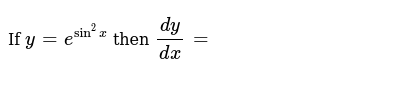



If Y E Sin 2x Then Dy Dx
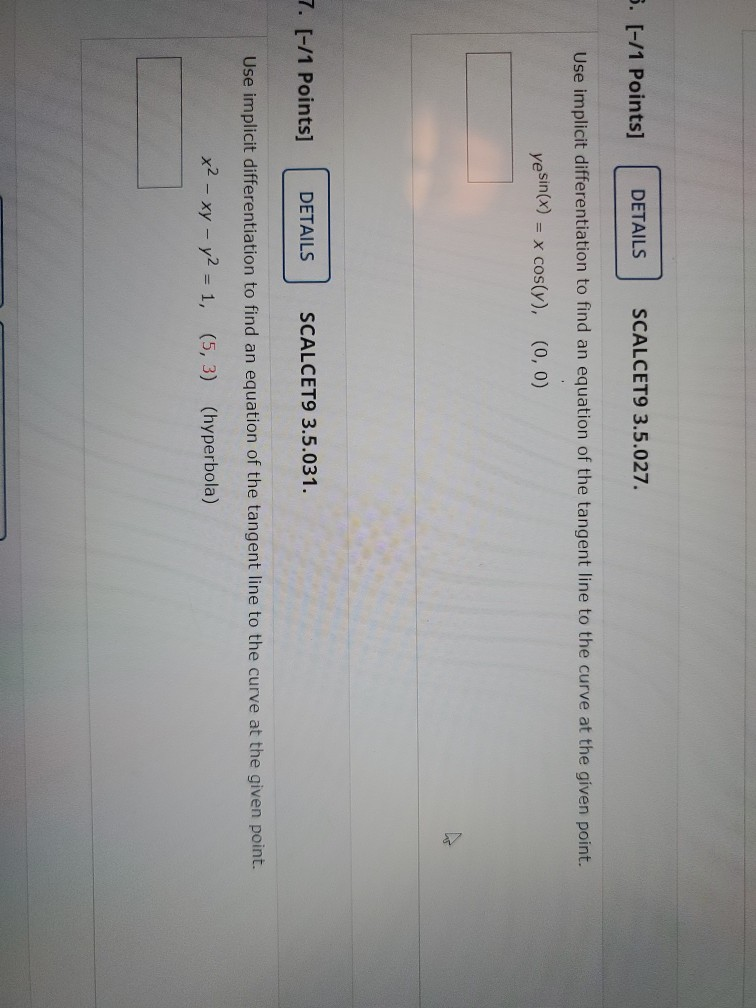



5 1 Points Details Scalcet9 3 5 027 Use Chegg Com
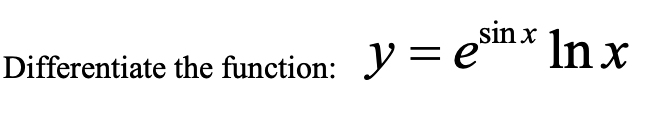



Answered Sin X In X Differentiate The Function Bartleby




Implicit And Logarithmic Differentiation




Find Dy Dx If Y E X Sin X Youtube




Ex 5 4 4 Differentiate Sin Tan 1 E X Chapter 5 Class 12
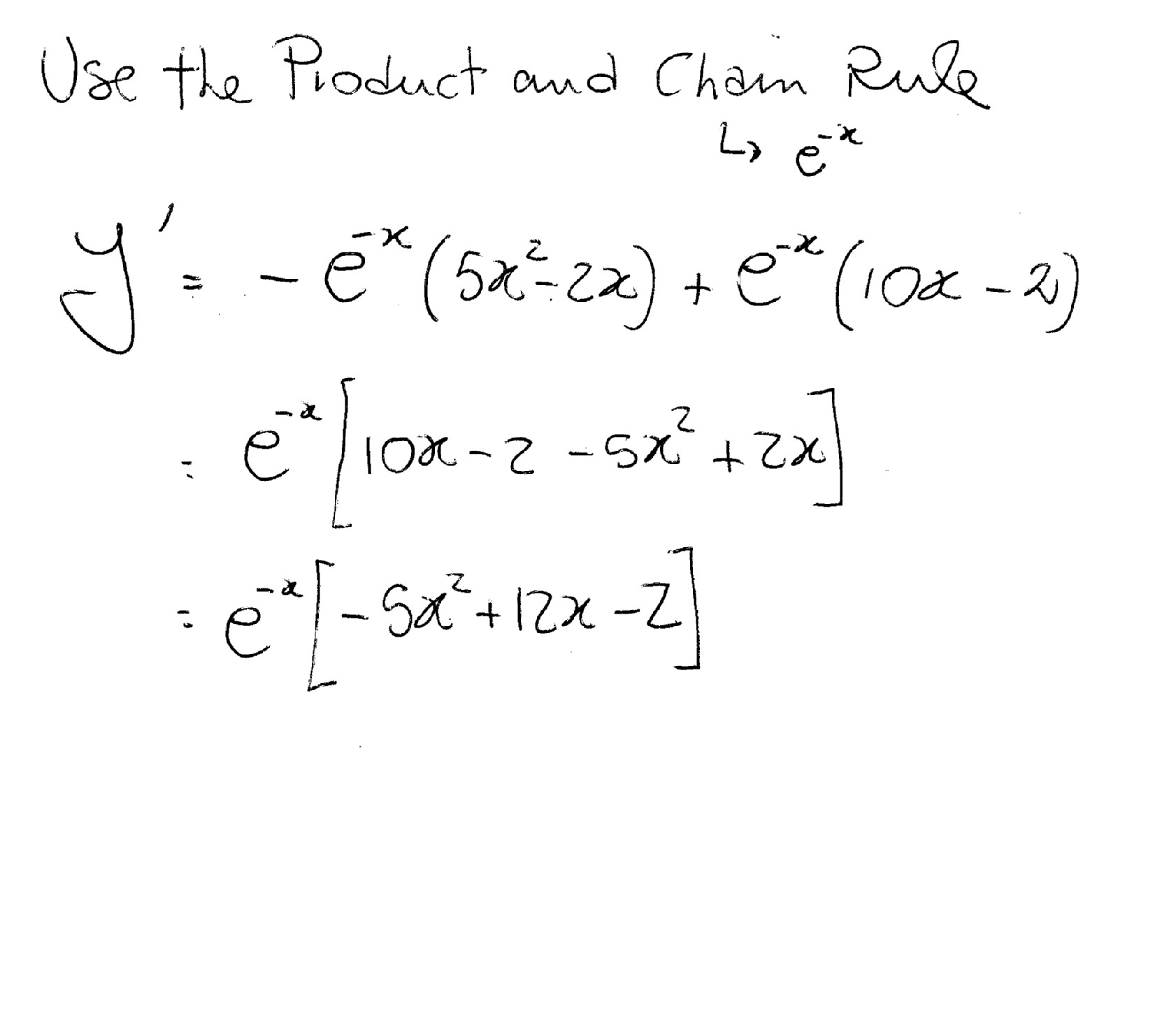



How Do You Find The Derivative Of Y E X 5x 2 2x Socratic




Find The Derivative Of E Sinx From The First Principle




Differentiate Sin 2x W R T E Cosx



What Is The Derivative Of Y E Cosx Sinx Quora




Find Dy Dx Y E 3x Sin4x 2 X




Ex 9 4 15 Find Equation Of Curve Passing Through 0 0




Differentiate E Sinx 2 With Respect To X



Find Dy Dx If Y E Sin 2 X 2tan 1 1 X 1 X Sarthaks Econnect Largest Online Education Community




Find The Derivative Of Each Of The Following 1 Y Chegg Com
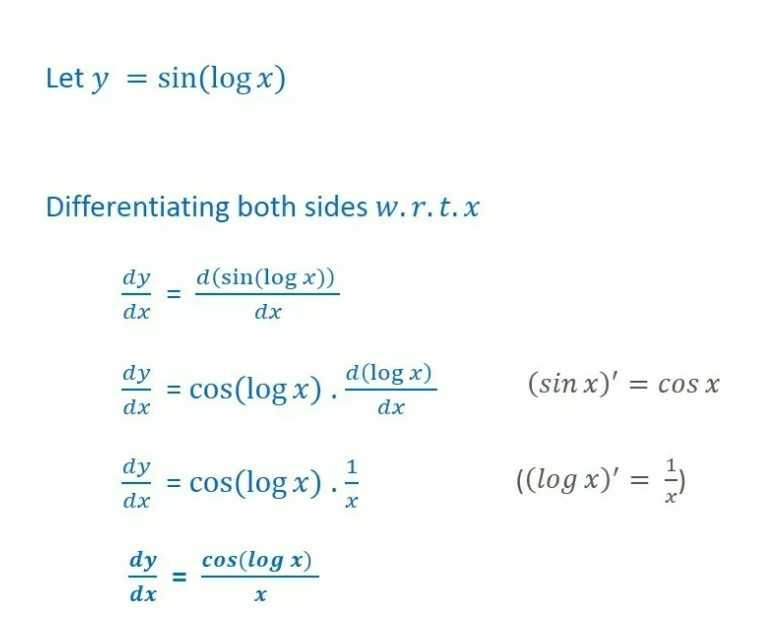



Y E X Sin Logx Find Dy Dx Scholr




Chain Rule E Sinx Differentiation Youtube




Find The Derivative Of E Sinx From The First Principle Youtube




Differentiate E Sinx With Respect To X By First Principal Maths Continuity And Differentiability Meritnation Com




1 Use The Implicit Differentiation To Find An Chegg Com



What Is The Nth Derivative Of E X Sinx Cos X Quora



How To Differentiate Math E Sin X Quora



1



If Y E X Sin X Then Prove That D 2y Dx 2 2dy Dx 2y 0 Sarthaks Econnect Largest Online Education Community




Ex 5 4 2 Differentiate E Sin 1 X Teachoo Ex 5 4




3 Differentiation Rules Differentiation Rules 3 4 The



What Is The Differentiation Of Ln Sinx Quora



How To Differentiate Math E Sin X Quora




If Y Ex Sin X Prove That D2y Dx2 2 Dy Dx 2y 0 Explain In Great Detail Mathematics Topperlearning Com 5p09j033




Y Log E X Sinx




Successive Differentiation Taylor S Maclaurine S Thm Studocu



How To Differentiate Math E Sin X Quora
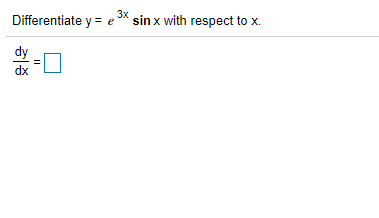



Solved 3x Differentiate Y E Sin X With Respect To X Dy Chegg Com



If Y X 3 E X Sin X Then Find Dy Dx Sarthaks Econnect Largest Online Education Community




Let Y E X Sin X 3 Tan X X Then Find Dy Dx Maths Differentiation Meritnation Com




Ppt Download



Differentiate And Simplify F X Sinx E 2x Physics Forums




Euler S Formula Wikipedia
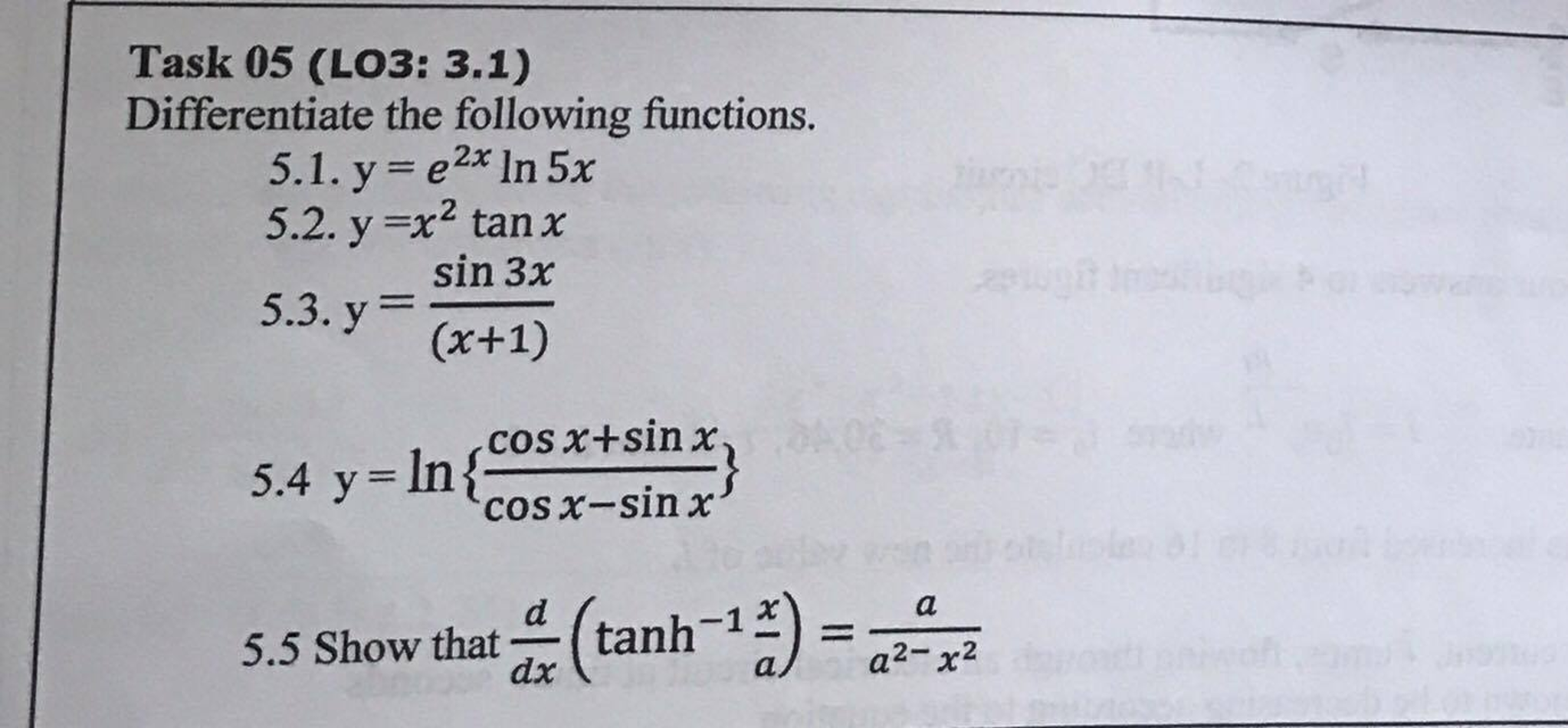



Differentiate The Following Functions Y E 2x Ln Chegg Com




Ex 5 7 6 Class 12 Maths Find Second Order Derivative Of E X Sin 5x




What Is The Nth Derivative Of Y E 2xsin3x I E E Power 2x Sin3x Quora




If Y E Sin X Then Dydx




If Y E Sinx Tan X X Prove That Dydx E Sinxcos X Tan X X 2x Cosec 2x Logtan X




Partial Differentiation




If Y E X Log Sin 2x Find Dy Dx




The Derivative Of The Function Y E Sin X Is 1 Chegg Com


